1. 트리(Tree) 구조
- 트리: Node와 Branch를 이용해서, 사이클을 이루지 않도록 구성한 데이터 구조
- 실제로 어디에 많이 사용되는가?
- 트리 중 이진트리(Binary Tree) 형태의 구조로, 탐색(검색) 알고리즘 구현을 위해 많이 사용됨
2. 알아둘 용어
- Node: 트리에서 데이터를 저장하는 기본 요소(데이터오 다른 연결된 노드에 대한 Branch 정보 포함)
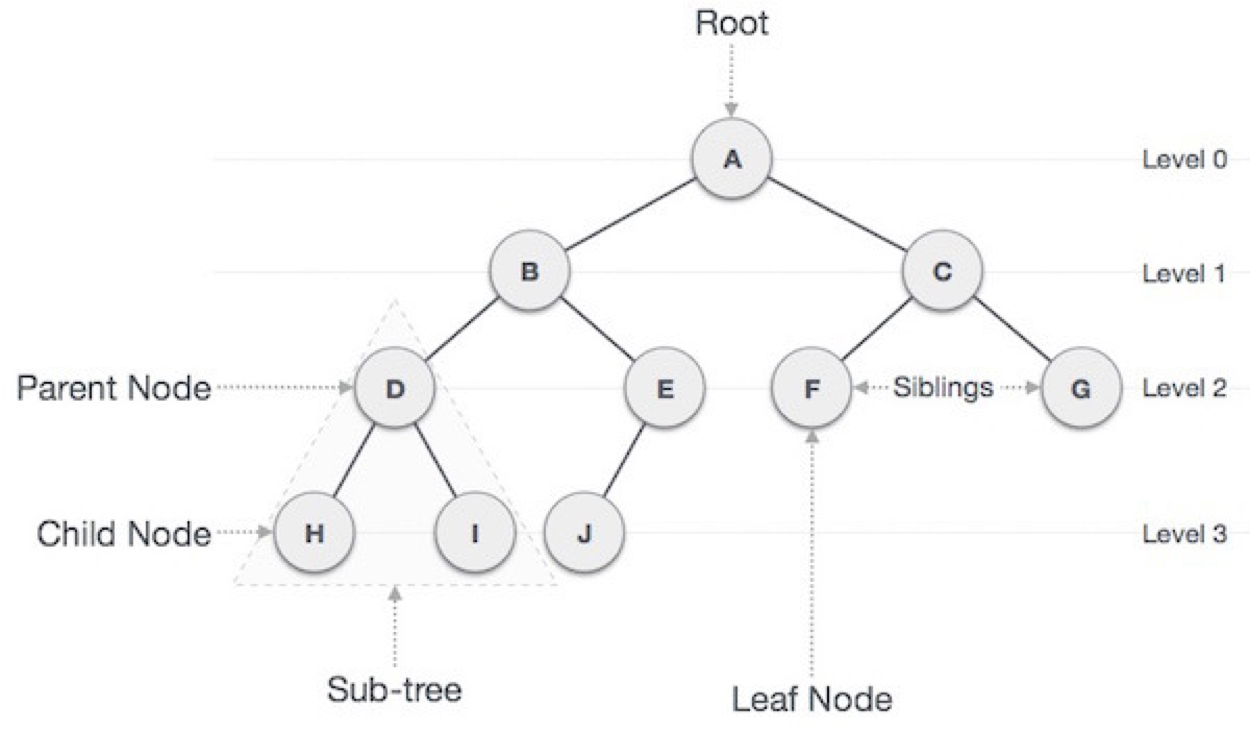
- Root Node: 트리 맨 위에 있는 노드
- Level: 최상위 노드를 Level 0 으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
- Parent Node: 어떤 노드의 다음 레벨에 연결된 노드
- Child Node: 어떤 노드의 상위 레벨에 연결된 노드
- Leaf Node(Terminal Node): Child Node가 하나도 없는 노드
- Sibling(Brother Node): 동일한 Parent Node를 가진 노드
- Depth: 트리에서 Node가 가질 수 있는 최대 Level
3. 이진 트리와 이진 트리 탐색(Binary Search Tree)
- 이지 트리: 노드의 최대 Branch가 2인 트리
- 이진 탐색 트리(Binary Search Tree: BST): 이진 트리에 다음과 같은 추가적인 조건이 있는 트리
- 왼쪽 노드는 해당 노드보다 작은 값, 오른쪽 노드는 해당 노드보다 큰 값을 가지고 있다
4. 자료 구조 이진 탐색 트리의 장점과 주요 용도
- 주요 용도: 데이터 검색(탐색)
- 장점: 탐색 속도를 개선할 수 있음
5. 구현하기(Java)
5-1 노드 클래스 만들기
public class NodeMgmt {
public class Node{
Node left;
Node right;
int value;
public Node(int data){
this.value = data;
this.left = null;
this.right = null;
}
}
}
5-2 이진 탐색 트리에 데이터 넣기
public class NodeMgmt{
Node head = null;
public class Node {
Node left;
Node right;
int value;
public Node(int data) {
this.value = data;
this.left = null;
this.right = null;
}
}
public boolean insertNode(int data) {
// CASE1: Node 가 하나도 없을 때
if (this.head == null) {
this.head = new Node(data);
} else {
// CASE2: Node 가 하나 이상 들어가 있을 때
Node findNode = this.head;
while (true) {
// CASE2-1: 현재 Node 의 왼쪽에 Node 가 들어가야할 때
if (data < findNode.value) {
if (findNode.left != null) {
findNode = findNode.left;
} else {
findNode.left = new Node(data);
break;
}
// CASE2-2: 현재 Node 의 오른쪽에 Node 가 들어가야할 때
} else {
if (findNode.right != null) {
findNode = findNode.right;
} else {
findNode.right = new Node(data);
break;
}
}
}
}
return true;
}
}
}
5-3 이진 탐색 트리 탐색
public class Node {
Node left;
Node right;
int value;
public Node (int data) {
this.value = data;
this.left = null;
this.right = null;
}
}
public class NodeMgmt {
Node head = null;
public boolean insertNode(int data) {
// CASE1: Node 가 하나도 없을 때
if (this.head == null) {
this.head = new Node(data);
} else {
// CASE2: Node 가 하나 이상 들어가 있을 때
Node findNode = this.head;
while (true) {
// CASE2-1: 현재 Node 의 왼쪽에 Node 가 들어가야할 때
if (data < findNode.value) {
if (findNode.left != null) {
findNode = findNode.left;
} else {
findNode.left = new Node(data);
break;
}
// CASE2-2: 현재 Node 의 오른쪽에 Node 가 들어가야할 때
} else {
if (findNode.right != null) {
findNode = findNode.right;
} else {
findNode.right = new Node(data);
break;
}
}
}
}
return true;
}
public Node search(int data) {
// CASE1: Node 가 하나도 없을 때
if (this.head == null) {
return null;
// CASE2: Node 가 하나 이상 있을 때
} else {
Node findNode = this.head;
while (findNode != null) {
if (findNode.value == data) {
return findNode;
} else if (data < findNode.value) {
findNode = findNode.left;
} else {
findNode = findNode.right;
}
}
return null;
}
}
}'Algorithm' 카테고리의 다른 글
| [알고리즘] 선택 정렬 (Selection Sort) (0) | 2023.01.16 |
|---|---|
| [알고리즘] 버블 정렬(Bubble Sort) (0) | 2023.01.16 |
| [알고리즘] 자료구조: 해쉬 (0) | 2022.12.07 |
| [알고리즘] 자료구조: 시간복잡도, 공간복잡도 (0) | 2022.12.06 |
| [알고리즘] 자료구조: 링크드 리스트(Linked List) (1) | 2022.12.05 |